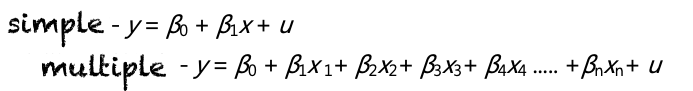最後更新時間 02/22/2022
Life is like a road. We will meet different people and face different issues. We do not always walk in the same direction, but usually take similar tactics or solutions, and a similar emotional response any time experience is repeated. If the person really does act in the repetitive ways described above, the resulting pattern could fit a linear regression that could predict his/her future.
First of all, what is “linear regression”? Linear regression is a graphic, line-based approach to modeling the relationship between a dependent variable (y) and one or more independent variables (x). The case of one independent variable (x) is called a simple linear regression. For two or more independent variables (x), the process is called multiple linear regression.
In modeling, the values of dependent variables depend on the values of independent variables. Independent variables (x) represent inputs or causes, that is, potential reasons for variation. These variables symbolize our academic major, friends, jobs, etc. The dependent variables represent the output or outcome whose variation is being studied, such as an individual’s life’s blueprint, which the number of independent variables determines the values of the dependent variable.
The main applications of linear regression have two broad categories: prediction and explanation. Here, I want to focus on prediction. In fact, real life applies it to predict people’s behaviors. For example, the bank will decide how high credit limits will extend to a person depends on his or her characteristics, such as educational background, occupation, consumer behavior, etc. Therefore, the key point of accuracy for any linear regression model that predicts a pattern hinges on how much do we really understand about that person.
Returning to mathematics, take a look at simple linear regression. The predictions of Y when plotted as a function of X form a straight line. Since multiple linear regression involves many dimensions, it’s hard to plot the results.
Let’s have a look at the following formulas:
In simple linear regression, a dependent variable is predicted from one independent variable. In multiple regression, the dependent variable is predicted by two or more independent variables. Notice the βo in the formula; we called βo the intercept parameter, which is the constant. It is often defined as the mean of the dependent variable when we set all of the independent variables in our model to zero, which means the value crosses the y-axis at the regression line. This pattern represents the unchangeable parts of our life, like gender and family.
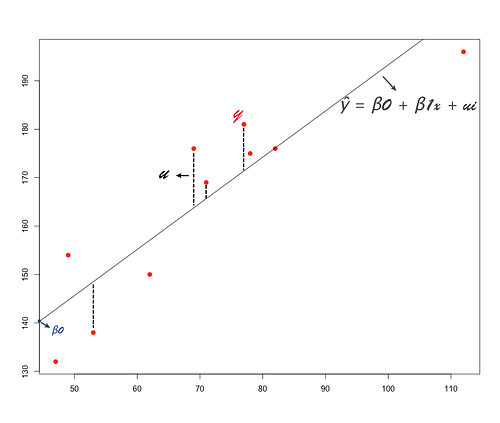
If the goal of a linear regression model is to explain variation in the response variable that can be attributed to variation in the independent variables, the intercept parameter becomes almost meaningless. Why? This is because you are not able to control the beginning of the life; the later elements represent independent variables which later altered the appearance and pattern of your life. For example, one’s the family (intercept parameter) has a limited impact on a person’s personality. However, after growing up, the elements (independent variables) such as society, friends, education, occupation are actually the key points in cultivating a person.
Now, take a look at the red point. The red point that deviates from the line is a measured variable which we called ‘y’; the red point that fits the line is the predicted value which we called ‘ŷ’. The error of prediction for a point is the value of the measured variable minus the predicted value. This part of the model is called the error term or disturbance term, which captures all other factors that impact the dependent variable y other than the independent variables x.
Think about it this way: we consider whole elements to put them all in the models and understand every response in any situation, such as if he is crying when he feels depressed; he screams when he is happy; he escapes when he encounters difficulties. However, sometimes an element changes by accident, such as when he is suddenly angry when he is upset; he is quiet when he feels great; he starts questioning when he faces dilemmas. The errors are more, and the accuracy of the model decreases.
Therefore, now that you’ve read my analysis, do you think is it possible to predict a person’s future by linear regression? It is not impossible, but it’s not easy. If most of the behaviors of a person are fixed, included his reaction to different conditions, social circle, work conditions, that we can recognize the pattern, the accuracy of a linear regression model is high. However, people do gradually change across the life span. When there are more errors in linear regression, the model may not be as good as it was meant to be anymore.
References and further reading:
https://en.wikipedia.org/wiki/Dependent_and_independent_variables
https://en.wikipedia.org/wiki/Linear_regression
http://onlinestatbook.com/2/regression/intro.html
https://statisticsbyjim.com/regression/interpret-constant-y-intercept-regression/
延伸閱讀:
如果你夠了解一個人,或許可以用線性迴歸預測他的未來 (中文版)
Life: Just Like Development of SQL to NoSQL
Ways the Job Search Process Resembles Machine Learning: Gradient Descent Helps Us to Get Dream Jobs