最後更新時間 02/22/2022
人生是條路,路上會遇到不同的人,面對不同的事,我們並非以始終如一的方向走,卻常常會用雷同的方式、解決方法、情緒面對諸多情況。如果真是如此同一個 pattern,其實我們可以用線性回歸預測未來。
首先,我先來說說什麼什麼是線性回歸(Linear regression),它是統計上自變數 x(Independent variable)和依變數 y(Dependent variable)之間關係建出來的模型。如果只有一個自變數 x 和一個依變數 y ,我們稱為簡單線性回歸(Simple linear regression),大於一個自變數 x ,則稱為多變量線性回歸(Multiple linear regression)。簡單來說,一個是一個 x 預測 y,一個是多個 x 預測 y。
自變數 x 獨立自主,不被其他變數影響,例如學業、朋友、工作,這是‘因’;依變數 y 基本上受到所有 x 的影響,只是被影響多和少的差別,能說是‘果’,可解釋為人生的藍圖,眾多元素 x 造就了人生 y。
建立線性回歸模型的目的在於預測,其實現實生活已經有人運用線性回歸預測人的行為,例如銀行根據一個人的基本資料、過去買賣行為判斷要給多少信用額度; 因此,在一個人身上做線性回歸的準確度關鍵在於我們了解這個人多少。我們了解自己多少。
回到數學層面,從圖來看,簡單線性單純是一條線,若要呈現多變量線性,因為它是多維度,所以畫不出來。
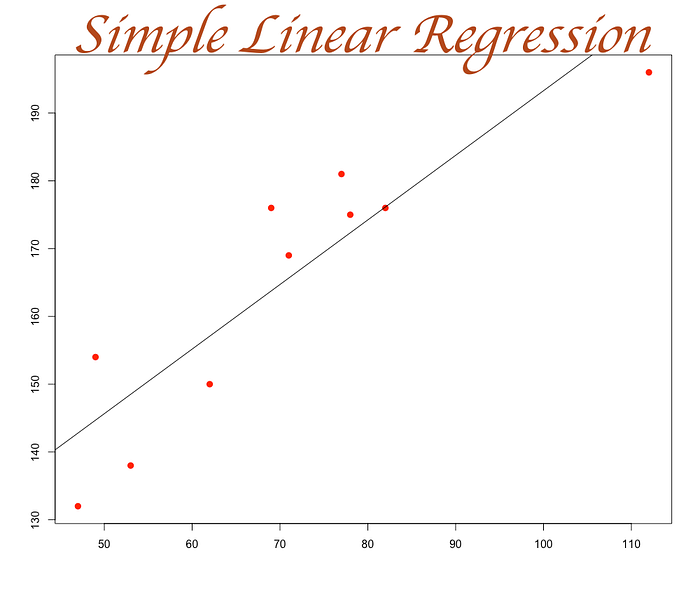
再來看一下公式:
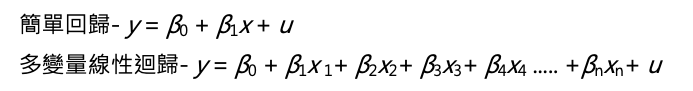
簡單線性是一個 x,多變量線性是多個 x。接著再注意公式中的 βo,βo 在統計學裡稱為截距項(Intercept parameter),也就是說當所有 x 都為 0 的時候,βo 為在 y 上面的那個點,我將它解釋成人生裡無法自己改變的部分,例如性別、原生家庭。
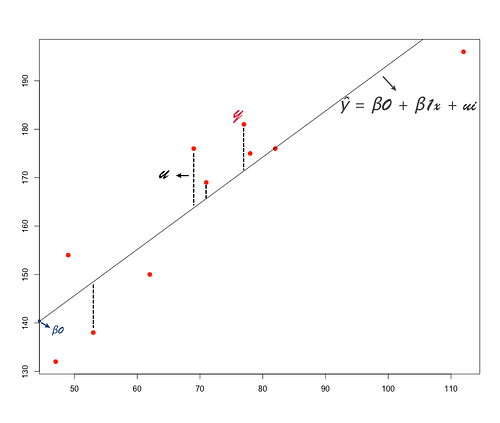
當我們利用統計分析軟體 R 跑線性回歸的時候,從觀察角度來說我們不太在意截距項,因為後面能影響結果 y 的變因 x 們遠遠大過截距項 βo。就像是人生開始的時候不是自己控制,後面的點點滴滴才是塑成現在你的樣子。不過嚴謹一點說,模型作為預測用並非觀察用,截距項就還是重要,只是相較沒那麼重要。換句話說,原生家庭可能會影響一個人的個性,但是長大後,社會、朋友、教育、工作等等變因才是會是塑成一個人全貌的關鍵。
接著看紅色點,線外紅色點是實際值 y,線上紅色點是 ŷ ,它是預測出來的,實際值減去預測值會有一個誤差值,也就是 u,我們稱之誤差項(Error term) 或干擾項(Disturbance),它代表著除了 x 之外其他可能會影響 y 的原因。想想用盡功夫把人生的各種元素加進去,遇到的情況會有的反應我們都撩落指掌,像是這人難過時會一直哭、開心時一直尖叫、遭遇困難就逃跑,然而有些意外你無法想到,可能他忽然難過時開始暴怒,開心時一直大笑、遭遇困難開始面對解決問題,當誤差很多,模型的準確率就會下降。
所以人生能不能用線性回歸預測呢?不是不可能,只是不容易。如果一個人的 pattern 已經固定了,了解他面對事情的反應、走向、平時的生活圈、工作內容,看得到循環,那回歸用在他身上準確率就是高的。可是人會改變,隨著時間、經歷、突然意外造成的成長或變化都是讓誤差值變大的因素,而回歸預測的樣子就不一定對了。
延伸閱讀:
Is it possible to predict a person’s future by linear regression? (English version)
Life: Just Like Development of SQL to NoSQL
Ways the Job Search Process Resembles Machine Learning: Gradient Descent Helps Us to Get Dream Jobs


